bojian_cc_20240918192332238377已知函数 $f(x)=x^2 \mathrm{e}^{-x}$, 若关于 $x$ 的方程 $f(x)=k$ 有唯一的实数根, 求 $k$的取值范围。
bojian_cc_20240918192421767090\text { 讨论 } g(x)=a \mathrm{e}^x-\ln x-1 \text { 的零点个数。 }
已知函数 $f(x)=2 \ln x, g(x)=x+2$, 若 $f\left(x_1\right)$ $=g\left(x_2\right)$, 求$x_2-2 x_1$ 的最大值.
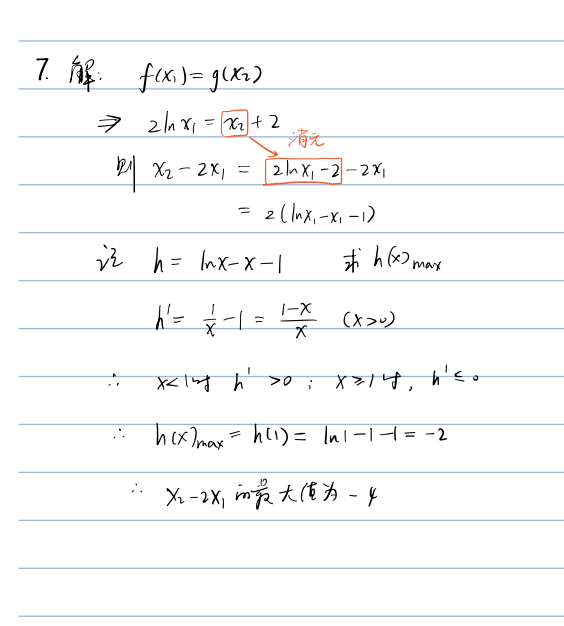
若函数 $f(x)=\frac{1}{2} x^2-x+a(x+\ln x)$ 没有极值,求实数 $a$ 的取值范围.

若函数 $g(x)=\dfrac{\ln x}{x+1}$ 在区间 $[t,+\infty)\left(t \in \mathbf{N}^*\right)$ 上存在极值, 求实数 $t$的最大值.
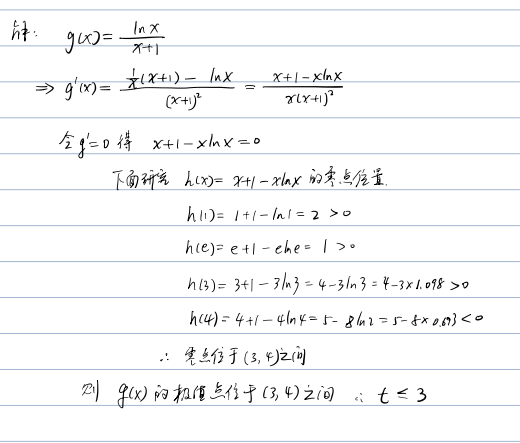
下面这道题目给我们的启示是:不要暴力求解含参不等式。本题已经得出了参数的取值范是$a \leq 0$,并且$g'$表达式中有我们熟悉的对勾函数形式$\dfrac{2}{x}+2x$,应该考虑参变分离。
若函数 $f(x)=\mathrm{e}^x-a x-1(a \in \mathbf{R})$ 为增函数, 则 $g(x)=2 \ln x+x^2-(a+2) x$ 的单调递增区间为?

已知函数 $f(x)=$ $\mathrm{e}^x-\cos x$, 设 $g(x)=x f^{\prime}(x)-f(x)$.
(1) 证明: $g(x)$ 在 $(0,+\infty)$ 上单调递增;
(2) 判断 $3 f\left(\dfrac{1}{3}\right)$ 与 $4 f\left(\dfrac{1}{4}\right)$ 的大小关系, 并加以证明。
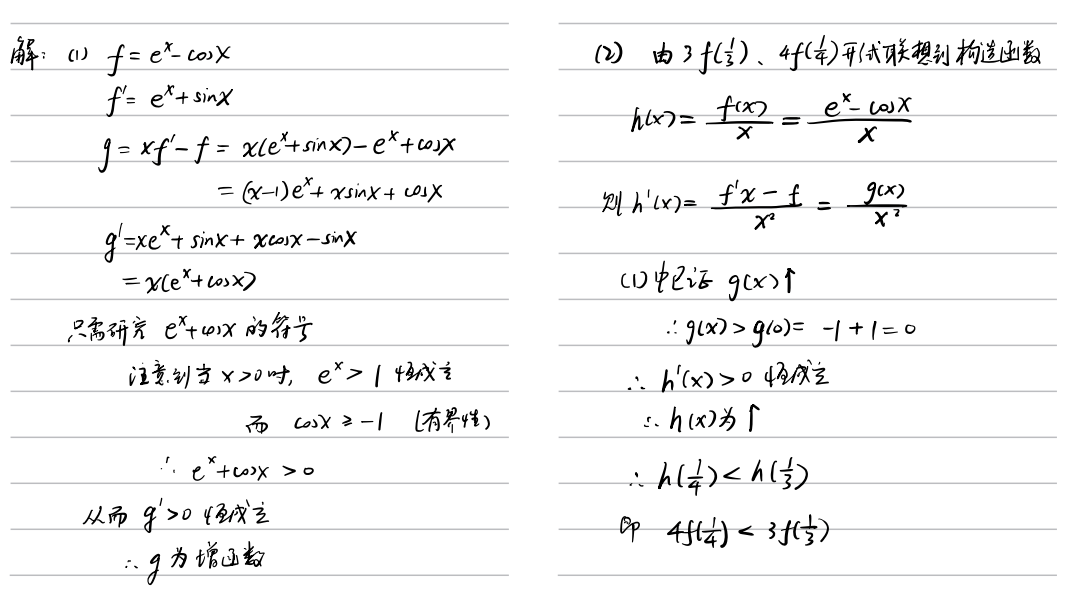
已知函数 $f(x)=$ $\ln x-a x$ 。
(1)讨论 $f(x)$ 的单调性;
(2) 当 $x \geqslant \dfrac{1}{\mathrm{e}}$ 时, $x f(x) \leqslant-x+a-1$, 求实数 $a$的取值范围.

声明:本文为原创文章,版权归剥茧自主学习所有,欢迎分享本文,转载请保留出处!
你可能也喜欢
- ♥ 高中物理答疑【力学综合篇】09/27
- ♥ 斜面受力分析的动画演示10/04
- ♥ 高一数学:解指数方程和对数方程10/14
- ♥ 物理演示实验:圆孔衍射10/20
- ♥ 高二物理答疑:电场的叠加10/05
- ♥ 高一数学答疑:建系计算向量问题09/30